Materi Ukuran Letak Data (Kuartil)

 

Materi Ukuran Letak Data

Pengetian Kuartil

Kuartil ialah suatu nilai – nilai yang membagi data yang telah diurutkan ke dalam empat bagian yang nilainya sama besar. Dalam menentukan letak kuartil data tunggal, kita harus melihat kondisi jumlah data (n) terlebih dahulu begitu juga sama halnya dengan cara menentukan kuartil data kelompok.

Kuartil pada suatu data dapat didapatkan dengan cara membagi data tersebut secara terurut kedalam empat bagian yang memiliki nilai sama besar.

Kuartil itu sendiri terdiri atas tiga macam, yaitu diantaranya:

  1. Kuartil bawah (Q1)
  2. Kuartil tengah / median (Q2)
  3. Kuartil atas ( Q3)

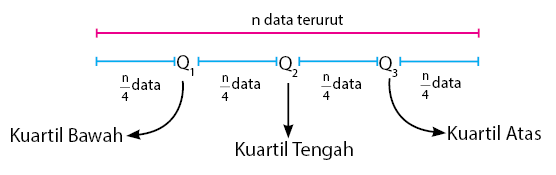
Dan apabila suatu data dilambangkan dengan garis lurus, letak kuartil bawah, kuartil tengah dan kuartil atas ialah sebagai berikut:

kuartil

Berdasarkan gambar diatas, bawah dapat kita ketahui letak – letak kuartilnya, yaitu pada kuartil bawah (Q1), kuartil tengah (Q2) dan kuartil atas (Q3)

Rumus Kuartil Untuk Nilai Data Tunggal

Berdasarkan pengertian kuartil diatas, maka dapat kita ketahui bahwa kuartil adalah membagi data menjadi empat bagian sama banyak. Oleh kaena itu, terdapat tiga nilai kuartil yang membagi data tersebut.

Sebelum melakukan pembagian data, pastikan bahwa data tersebut sebelumnya sudah kita urutkan terlebih dahulu. Untuk lebih jelasnya dapat dilihat ilustrasi dibawah berikut:

Nilai Kuartil Data Tunggal

Dalam mencari nilai kuartil untuk data tunggal, Rumus dibedakan menjadi dua kasus, yaitu: untuk jumah data ganjil dan jumlah data genap.

Untuk n ganjil, yaitu:

Sedangkan cara untuk mencari n genap, yaitu:

Langkah – langkah mencari tiga nilai kuartil data tunggal untuk jumlah data genap ialah sebagai berikut:

  1. Carilah nilai yang menjadi nilai tengahnya (median atau Q_{2}).
  2. Membagi data di sebelah kiri median menjadi dua bagian yang sama dan menghasilkan kuartil bawah atau Q_{1}.
  3. Membagi data di sebelah kanan median menjadi dua bagian yang sama dan menghasilkan kuartil atas atau Q_{3}.

Contoh Soal:

Perhatikanlah tabel data nilai matematika yang diperoleh sekelompok siswa dibawah berikut:

Contoh soal kuartil data tunggal

Pembahasan:

Langkah pertama:

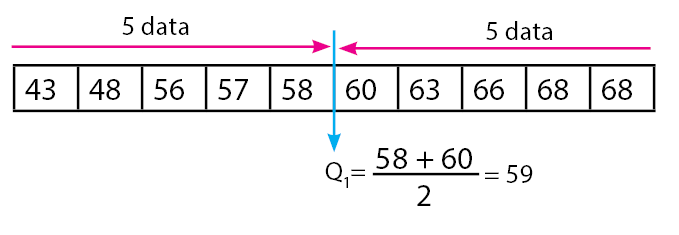
Urutkan data dan carilah nilai mediannya. Kemudian data yang telah diurutkan dan nilai median dapat dilihat pada gambar di bawah berikut:

Kuartil data tunggal

Selanjutnya, carilah nilai kuartil bawahnya (Q_{1}), maka diperoleh dari nilai tengah dari data terurut di sebelah kiri median, yaitu:

Kuartil bawah data tunggal

Maka, nilai kuartil bawahnya ialah 59

Rumus Kuartil Untuk Data Kelompok

Untuk mencari nilai kuartil untuk data kelompok, maka dapat di cari dengan menggunakan rumus sebagai berikut:

Qi = Tbi + (((i/4)n – Fi)/fi)c

Keterangaannya :
Tbi adalah Tepi bawah kuartil ke-i
Fi adalah Jumlah frekuensi sebelum frekuensi kuartil ke-i
fi adalah Frekuensi kuartil ke-i. i = 1, 2, 3
n adalah Jumlah seluruh frekuensi
C adalah Panjang interval kelas

Contoh Soal:

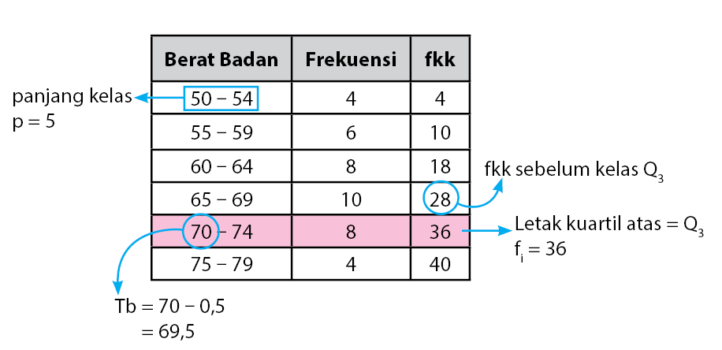
Perhatikan tabel di bawah berikut ini:

Contoh Soal Kuartil Data Kelompok

Tentukan kuartil atas pada tabel tersebut adalah :

Pembahasannya:

Kuartil atas ialah disimbolkan Q_{3}
Jumlah data yaitu:

  \[ = 4 + 6 + 8 + 10 + 8 + 4 \]

  \[ = 40 \]

Letak kuartil atas berada di  \frac{3}{4}  bagian data. Sehingga, letak kuartil atas tersebut berada di data ke-30. Maka caranya adalah sebagai berikut:

  \[ = \frac{3}{4} \times 40 \]

  \[ = 30 \]

Selanjutnya, perhatikanlah tabel yang sudah dilengkapi dengan frekuensi komulatif kurang dari (fkk) dan letak kuartil atas, yaitu:

Kuartil atas data kelompok

Sehingga, nilai kuartis atasnya ialah:

  \[ Q_{3} = 69,5 + \left( \frac{\frac{3}{4} \cdot 40 - 28 }{36} \right) \times 5 \]

  \[ Q_{3} = 69,5 + \left( \frac{30 - 28 }{36} \right) \times 5 \]

  \[ Q_{3} = 69,5 + \left( \frac{2}{36} \right) \times 5 \]

  \[ Q_{3} = 69,5 + 0,28 = 69,78 \]

Lokasi: Bengkulu, Bengkulu City, Bengkulu, Indonesia

Komentar

Posting Komentar